Matrizen
Definition: Eine m x n -Matrix ist ein Zahlenschema mit m Zeilen und n Spalten.
allgemeines Beispiel:
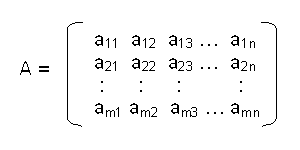
Eine einzelne Zahl (a11, a12 usw.) in der Matrix wird als Matrixelement bezeichnet.
Besondere Matrizen:
- Nullmatrix: alle Matrixelemente sind Null
- quadratische Matrix: Zeilenzahl gleich Spaltenzahl
- Transponierte Matrix: Zeilen und Spalten werden miteinander vertauscht
Rechenregeln:
1. Addition:
A + B = aik + bik
für i=1,2...,m und k=1,2,...,n
d.h. Matrixelemente mit gleichem Index werden addiert. Das Ergebnis ist erneut eine Matrix.
2. Subtraktion:
A - B = aik - bik
für i=1,2...,m und k=1,2,...,n
d.h. Matrixelemente mit gleichem Index werden subtrahiert. Das Ergebnis ist erneut eine Matrix.
3. Multiplikation mit einem Skalar(Zahl):
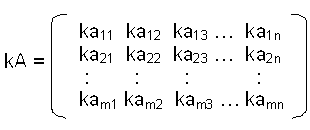
für k Element der komplexen Zahlen
d.h. jedes Matrixelement wird einzeln mit dem Skalar multipliziert.
4. Multiplikation mit einem Vektor:
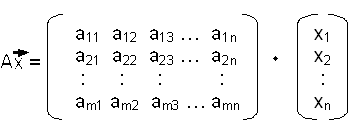
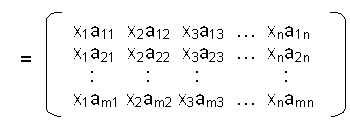
Wichtig: Spaltenzahl der Matrix muss gleich der Dimension des Vektors sein, sonst ist diese Rechenoperation nicht möglich.(m x n -Matrix und Vektor des Rn)
5. Multiplikation mit einer Matrix:
Ist A eine m x n - Matrix und B eine n x p - Matrix, so erhalten wir für A·B eine m x p -Matrix C.
Daraus folgt A?B ungleich B·A.
Ein solches Matrizenprodukt A·B lässt sich am einfachsten mit dem FALK-Schema (bzw. FALKsches Schema) berechnen.
allemeines Beispiel für ein FALK-Schema:

Die Werte der Matrixelemente von C werden aus dem Skalarprodukt des zugehörigen Zeilenvektors von A bzw. Spaltenvektors von B gebildet.
Bsp.: c22 = a21b12 + a22bb22 + ... + a2nbn2

