Vektorrechnung
Aus Gründen der Vereinfachung der Schreibweise wird auf dieser Seite zum Thema Vektorrechnung auf einen Pfeil über den Vektoren verzichtet.
Definition: Bei Vektoren handelt es sich um gerichtete Größen, welche durch Betrag (Länge) und Richtung vollständig beschrieben sind.
Schreibweise:
Vektoren lassen sich in folgender Form schreiben:
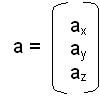
a = (ax / ay / az) bzw. a = (ax ; ay ; az)
ax , ay und az werden als Komponenten bezeichnet. Die Anzahl der Komponenten gibt Auskunft über den Vektorraum des Vektors a. In diesem Fall ist der Vektor a ein Vektor des R3.
Ein Vektorraum kann allgemein als Rn geschrieben werden. (n=1,2,3...)
Rechenregeln:
|a| = √(ax2 + ay2 + az2) Betrag
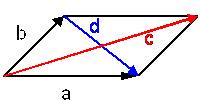
a + b = c (ax + bx / ay + by / az + bz) Addition
a - b = d (ax - bx / ay - by / az - bz) Subtraktion
Geometrische Bedeutung der Vektoraddition und Vektorsubtraktion:
ka = k(ax / ay / az) = (kax / kay / kaz) Multiplikation mit Skalar (Zahl)
Skalarprodukt:
a · b = (ax / ay / az) · (bx / by / bz) = axbx + ayby + azbz
Beachte: Das Ergebnis des Skalarprodukts ist ein Skalar (Zahl)
Vektorprodukt (Kreuzprodukt):
a x b = (ax / ay / az) x (bx / by / bz) =
= (aybz - azby / azbx - axbz / axby - aybx)
Eigenschaften des Vektorprodukts:
für a x b = c gilt:
- c senkrecht zu a und b
- a, b und c bilden ein Rechtssystem( vgl. Koordinatensystem)
Winkel zwischen zwei Vektoren:
cos φ = (a · b)/(|a| · |b|)

