Wellenlehre - Eigenschwingung
Bei einem Medium mit bestimmter Geometrie und festen Randbedingungen kann eine stehende Welle erzeugt werden, wenn die Wellenl?nge auf die geometrischen Eigenschaften abgestimmt ist. Nach der Anregung entsteht die stehende Welle (Eigenschwingung) durch sich wiederholende Reflexionen an den geometrischen Grenzen und deren Überlagerung mit den einlaufenden Wellen.
Lage von Wellenknoten und Wellenbauch in Abhängigkeit von den Randbedingungen:
- Reflexion am freien Ende -> Wellenbauch
- Reflexion am festen Ende -> Wellenknoten
Anhand des folgenden Beispiels (eingespannter Metallstab) sollen nun die Formeln für die Wellenlänge und die Eingenfrequenzen bestimmt werden.
Randbedingungen: ein freies Ende, ein festes Ende (Einspannung)
Über die Länge L des Stabes werden nun die ersten drei Eigenschschwingungen angetragen.
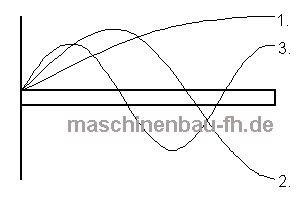
Die Wellenlängen lassen sich nun über den Vergleich mit folgendem Wellenbild bestimmen:
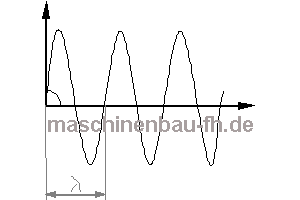
1. Eigenschwingung (kleinste Frequenz f, größte Wellenlänge λ)
L = λ1/4
λ1 = 4L
f1 = c/λ1 = c/4L
2. Eigenschwingung
L = 3/4 · λ2
λ2 = 4/3 · L
f2 = c/λ2 = c/4L · 3
3. Eigenschwingung
L = 5/4 · λ3
λ3 = 4/5 · L
f3 = c/λ3 = c/4L · 5
n-te Eigenschwingung
λn = 4L/(2n-1)
fn = c/λn = c/4L · (2n-1)
Analog lassen sich Wellenlänge und Eigenfrequenz für die Randbedingungen festes Ende - festes Ende (identisch mit frei-frei) bestimmen.
Es ergeben sich folgende Gleichungen für die n-te Eigenschschwingung:
λn = 2L/n
fn = c/2L · n
Aufgaben zur Eigenschwingung

